Algorithm - Disjoint Set
Created by : Mr Dk.
2021 / 01 / 11 21:42
Nanjing, Jiangsu, China
About
并查集 是一种树型的数据结构,用于处理一些不相交集合的合并。一些元素,从一开始各自属于一个集合,随着条件的逐渐给出,集合之间会互相合并,直到最终操作结束,不同元素可能会分属不同的集合。其中主要包括两个主要操作:
- 合并 - 把两个不相交的集合合并为一个集合
- 查询 - 查询两个元素是否属于一个集合
Theory
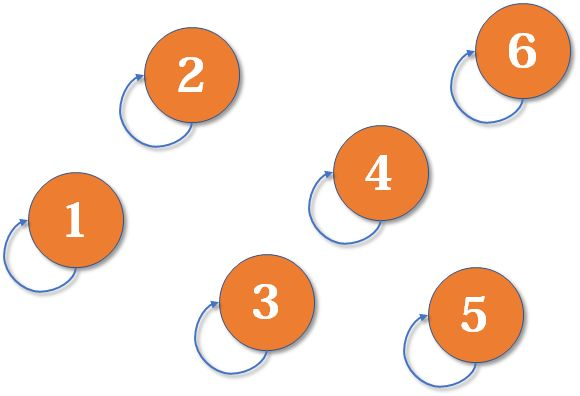
最开始,每个元素分属一个类型,可以初始化一个数组,数组中的每个元素分别代表一个类型:
vector<int> collection(length);
for (size_t i = 0; i < collection.size(); i++) {
collection[i] = i;
}
此时集合图示为:
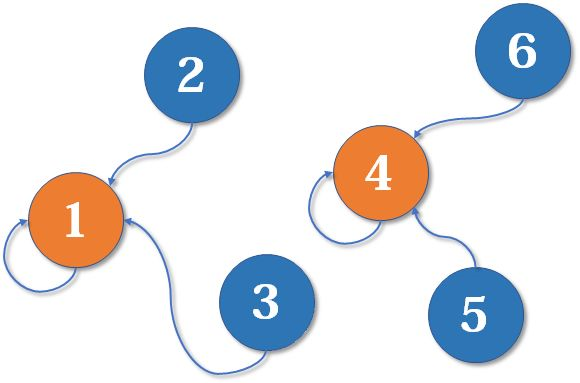
接下来,随着条件的给出 (比如元素 A 和元素 B 同属一类),分属不同集合的元素需要被合并到一个集合中:
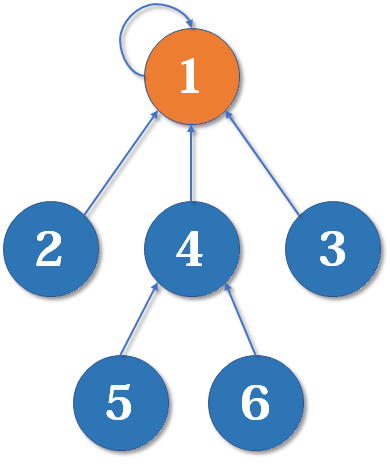
在每个集合中,都会有一个 代表元素 (即根结点)。只需要使元素中的代表元素指向要合并的元素,就能合并集合:
以上过程完全可以由一个数组来实现:
int find_root(vector<int> &collection, int i) {
return collection[i] == i ? i : find_root(collection, collection[i]);
}
实战中,有更好的
find_root()实现方式。
void merge() {
collection[find_root(i)] = find_root(j);
}
Path Compression
随着集合的合并,可能会导致形成越来越长的链,从而导致每次的 查询 操作耗时长。可以对路径进行压缩,从而优化查询操作的时间复杂度:

另一种实现的 find_root() 算法能够在合并分组的同时,顺便实现路径压缩。在递归结束后,顺便更新每个结点所在集合的 root 结点:
int find_root(vector<int> &collection, int i) {
return collection[i] == i ?
i :
collection[i] = find_root(collection, collection[i]);
}
在实际使用中,如果需要形成真正 unique 的并查集,在合并分组完成后,还要额外单独进行一轮路径压缩。这是由于 for 循环遍历的先后顺序导致的。
Rank
两个集合合并时,原则上应当使简单的集合并入复杂的结合中,这样到根结点的路径变长的结点数更少:
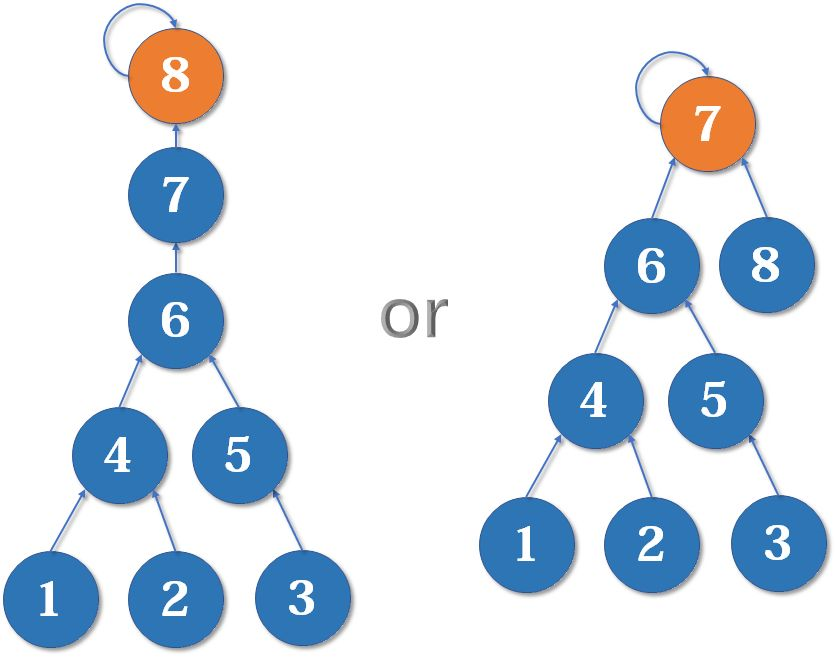
可以为每个结点维护一个 rank[] 数组,记录以每个结点为根的树深度。一开始所有元素的深度都为 1。合并时,把深度较小的结点往深度较大的结点上合并。
路径压缩和按秩合并同时启用时,树的深度将会变得不准确,但是总比没有按秩合并的性能要好。